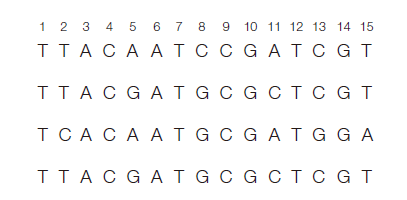群体遗传学概念
我的记忆力实在是太差了(金鱼?.?),为了更深一步的巩固自己的记忆,加深一些概念的理解,固有此。
本人能力有限,如理解有问题恳请及时纠正!
1. π (pi) 核苷酸多样性
用来衡量核苷酸多样性的大小,越大,说明群体多样性越高。目前主要有两种计算π的方法(只考虑biallelic sites: 群体在这个位点只存在两种核苷酸):
1.分离位点(群体在这个位点存在>=两个核苷酸)的位点杂合度之和:
$$ π = \sum_{1}^Sh_j $$
其中S为分离位点的个数,而$h_j$则是不同位点杂合度:
$$ h_j = \frac{n}{n-1}(1-\sum p^2_i)$$
$p_i$指的是不同核苷酸出现概率,二等分位点只存在两种情况。n指的样本数量。
2.任意两条序列之间核苷酸差异的平均位点数:
$$ π = \frac {\sum_{i<k}k_{ij}}{n(n-1)/2}
光看公式没什么感觉,手动算一下吧:
假设这里包含四个样本,一共15个位点的比对结果。
如果用第一种方法的话,这15个位点中包含6个分离位点: 2 5 8 11 13 15。由$h_j$的计算公式得:
$$
π = h_2 + h_5 + h_8 + h_{11} + h_{13} + h_{15}
\ = \frac {4}{3}(1-\frac{1}{4}^2 - \frac{3}{4}^2) + \frac {4}{3}(1-\frac{1}{2}^2 - \frac{1}{2}^2) + \frac {4}{3}(1-\frac{1}{4}^2 - \frac{3}{4}^2)+ \frac {4}{3}(1-\frac{1}{2}^2 - \frac{1}{2}^2) + \frac {4}{3}(1-\frac{1}{4}^2 - \frac{3}{4}^2) + \frac {4}{3}(1-\frac{1}{4}^2 - \frac{3}{4}^2) \ =0.5 + 0.667 + 0.5 + 0.667 + 0.5 + 0.5 \ = 3.33
$$
如果用第二种方法,我们这里一共有4个样本(4条序列),从这4条序列中抽取2条序列,一共有$C^2_4=6$种情况,这种情况下,这两种方法的π是一致的。
$$
π = (3 + 4 + 3 + 5 + 0 + 5) / 6 = 3.33
$$
在一般的分析中,我们通常算的是每一个窗口(通常5kbp、10kbp和50kbp)的平均π值,所以这里的每核苷酸$π=\frac {3.33}{15}=0.222$。在全基因水平上,通常使用第一种方法计算,第二种方法太耗时($C^2_n*w$ n:样本数 $w$:位点数目)。
References:
Tajima F. Statistical analysis of DNA polymorphism. Jpn J Genet. 1993 Dec;68(6):567-95. doi: 10.1266/jjg.68.567. PMID: 8031577.
2. 搭便车效应(Hitchhiking Effect)
一个有利突变在正向选择的作用下会迅速增加其在群体内的频率,同时因为连锁不平衡,会导致离他物理位置很近的一些基因型的频率也提高了。
这会造成所谓的”选择扫荡”,这里简单的考虑两种情况:Hard sweeps和Soft sweeps。
- Hard sweeps:
如图A所示,当群体中某个样本突然产生了一个对环境非常有利的突变,因为正向选择作用,这个突变位点+和它连锁的位点在群体内会迅速fixed,形成单一的haplotype。 - Soft sweeps:如图B所示,可能是由于环境的突然变化,导致群体中已经存在的某个有利基因型被迅速fixed,但因为这个有利基因型已经存在于不同的haplotype block里面了。所以最后这个区域可能只存在具有这个有利基因型的haplotype了(图中2种)。
选择扫荡会大大降低群体核苷酸的多样性,驯化的人为选择也会导致选择扫荡的产生,我们通过找到这些选择扫荡区域,就有可能找到一些与重要驯化农艺性状相关的基因。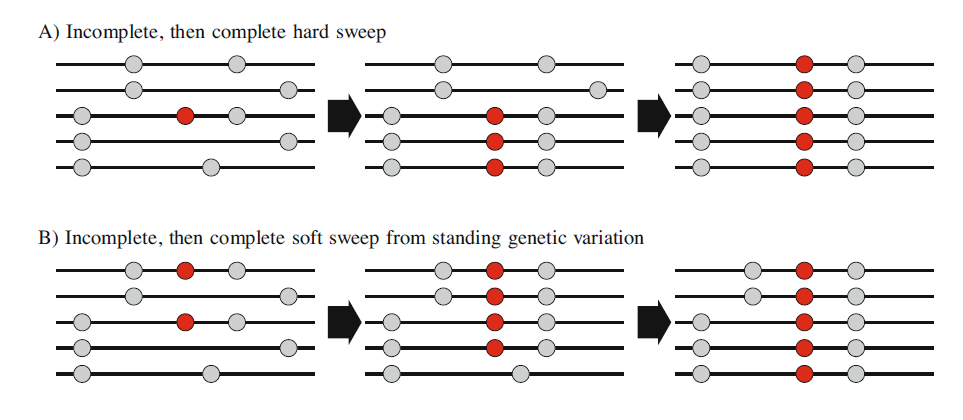
3. 连锁不平衡(Linkage Disequilibrium)
4. 重组交换(Recombination)
References: